XXH3 - a new speed-optimized hash algorithm
The xxHash family of hash functions has proven more successful than anticipated. Initially designed as a checksum companion for LZ4, it has found its way into many more projects, requiring vastly different workloads.
I was recently summoned to investigate performance for a bloom filter implementation, requiring to generate quickly 64 pseudo-random bits from small inputs of variable length. XXH64 could fit the bill, but performance on small inputs, never was its priority. It’s not completely wasteful either, it pays a bit attention to short inputs thanks to a small speed module in SMHasher. However, the module itself does the bare minimum, and it was not clear to me what’s exactly measured.
So I decided to create my own benchmark program, as a way to ensure that I understand and control what’s being measured. This was a very interesting journey, leading to surprising discoveries.
The end result of this investigation is XXH3, a cross-over inspired by many other great hash algorithms, which proves substantially faster than existing variants of xxHash, across basically all dimensions.
Let’s detail those dimensions, and give some credit where inspiration is due.
Checksumming long inputs
xxHash started as a fast checksum for LZ4, and I believe it can still be useful for this purpose. It has proven popular among movie makers for file transfer verification, saving a lot of time thanks to its great speed. The main downside is that XXH64() is limited to 64-bit, which is insufficient when comparing a really large number of files (and by large I mean many many million ones). For this reason, a 128-bit variant has often been requested,
XXH3 features a wide internal state of 512 bits, which makes it suitable to generate a hash of up to 256 bit. For the time being, only 64-bit and 128-bit variants are exposed, but a similar recipe can be used for a 256-bit variant if there is any need for it one day. All variant feature same speed, since only the finalization stage is different.
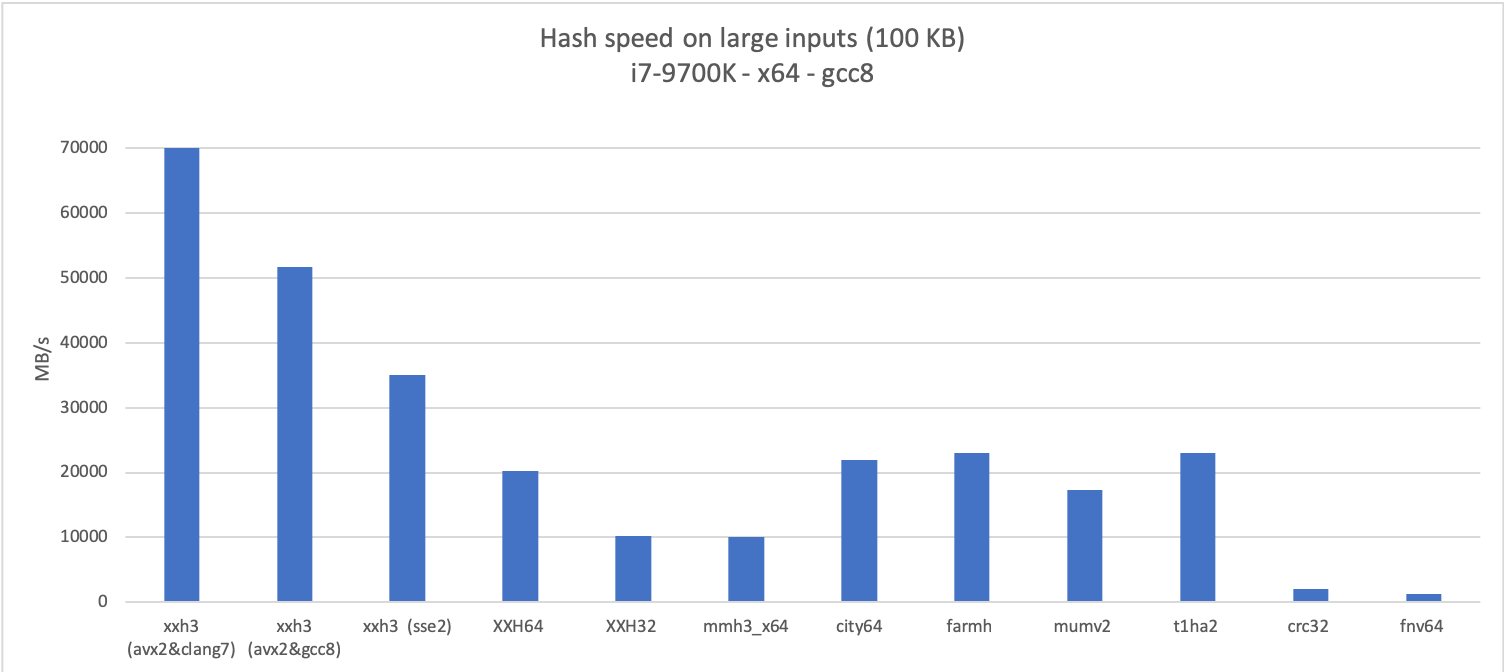
I’m using this opportunity to compare with a few other well known hash algorithms, either because their notoriety makes them frequently named in discussions related to hash algorithms (FNV, CRC), or because they are very good in at least one dimension.
XXH3 proves very fast on large inputs, thanks to a vector-friendly inner-loop, inspired Bulat Ziganshin’s Farsh, itself based on UMAC paper.
Unfortunately, UMAC features a critical flaw for checksumming, which makes it ignore 4 bytes of input, on average every 16 GB. This might not seem much, and it might even be acceptable if the goal is to generate a 32-bit checksum as in the original paper. But for checksumming large files with 64-bit or 128-bit fingerprints, this is a big no-no.
So the version embedded into XXH3 is modified, to guarantee that all input bytes are necessarily present in the final mix. This makes it a bit slower, but as can be seen in the graphs, it remains plenty fast.
Vectorization must be done manually, using intrinsic, as the compiler seems unable to properly auto-vectorize the scalar code path.
For this reason, the code offers 4 paths : scalar (universal), SSE2, AVX2, and also NEON offered by Devin Hussey. It may be possible to vectorize additional platforms, though this requires dedicated efforts.
SSE2 is enough to reach substantial speed, which is great because all x64 cpus necessarily support this instruction set. SSE2 is also free of dynamic throttling issues, and is automatically enabled on all x64 compilers. Hence I expect it to be the most common target.
On a given code path, compilers can make a difference. For example, AVX2 vectorization is significantly more effective with clang. Actually, the speed of this variant is so fast that I was wondering if it was faster than my main memory. So I graphed the speed over a variety of input sizes.

As one can see, the AVX2 build is much faster than main memory, and the impact of cache size is now clearly observable, at 32 KB (L1), 256 KB (L2) and 8 MB (L3). As a rule, “top speed” is only achievable when data is already in cache.
So is it worth being so fast ?
If data is very large (say, a movie), it can’t fit in the cache, so the bottleneck will be at best the main memory, if not I/O system itself. In which case, a faster hash may save cpu time, but will not make the checksumming operation faster.
On the other hand, there are many use cases where data is neither large nor small, say in the KB range. This includes many types of record, typical of database workloads. In these use cases, hashing is not the main operation : it’s just one of many operations, sandwiched between other pieces of code. Input data is already in the cache, because it was needed anyway by these other operations. In such a scenario, hashing faster helps to a faster overall run time, as cpu savings are employed by subsequent operations.
32-bit friendliness
The computing world is massively transitioning to 64-bit, even on mobile. The remaining space for 32-bit seems ever shrinking. Yet, it’s still present, in more places than can be listed. For example, many virtual environment generate bytecodes designed to produce a 32-bit application.
Thing is, most modern hash algorithms take advantage of 64-bit instructions, which can ingest data twice faster, so it’s key to great speed. Once translated for the 32-bit world, these 64-bit instructions can still be emulated, but at a cost. In most cases, it translates into a massive speed loss. That’s why XXH32 remains popular for 32-bit applications, it’s a great performer in this category.
A nice property of XXH3 is that it doesn’t lose so much speed when translated into 32-bit instructions. This is due to some careful choices in instructions used in the main loop. The result is actually pretty good :

XXH3 can overtake XXH32, even without vectorial instruction ! Enabling SSE2 put it in another league.
A similar property can be observed on ARM 32-bit. The base speed is very competitive, and the NEON vectorial code path designed by Devin makes wonder, pushing speed to new boundaries.
Hashing small inputs
The high speed achieved on large input wasn’t actually the center of my investigation.
The main focus is about short keys of random lengths, with a distribution of length roughly in the 20-30 bytes area, featuring occasional outliers, both tiny and large.
This scenario is very different. Actually, with such small input, the vectorized inner loop is never triggered. Delivering a good quality hash result must be achieved using a small amount of operations.
This investigation quickly converged onto Google’s CityHash, by Geoff Pyke and Jyrki Alakuijala. This algorithm features an excellent access pattern for small data, later replicated into FarmHash, giving them an edge. This proved another major source of inspiration for XXH3.
A small concern is that Cityhash comes in 2 variants, with or without seed. One could logically expect that both variants are “equivalent”, with one just setting a default seed value.
That’s not the case. The variant without seed forego the final avalanche stage, making it faster. Unfortunately, it also makes it fail SMHasher’s avalanche test, showing very large bias. For this reason, I will distinguish both variants in the graph, as the speed difference on small inputs is quite noticeable.
The benchmark test looks simple enough : just loop over some small input of known size, and count the nb of hashes produced. Size is only known at run time, so there’s no way for the compiler to “specialize” the code for a given size. There are some finicky details in ensuring proper timing, but once solved, it gives an interesting ranking.

Top algorithms are based on the same “access pattern”, and there are visible “steps” on reaching 33+ length, and then again at 65+. That’s because, in order to generate less branches, the algorithm does exactly the same work from 33 to 64 bytes. So the amount of instructions to run is comparatively large for 33 bytes.
In spite of this, XXH3 maintains a comfortable lead even at “bad” length values (17, 33, 65).
This first results looks good, but it’s not yet satisfying.
Remember the “variable size” requirement ?
This is not met by this scenario.
Impact of variable input sizes
Always providing the same input size is simply too easy for branches. The branch predictor can make a good job at guessing the outcome every time.
This is just not representative of most real-life scenarios, where there’s no such predictability. Mix inputs of different sizes, and it wreaks havoc on all these branches, adding a considerable cost at each hash. This impact is often overlooked, because measuring it is a bit more difficult. But it’s important enough to deserve some focus.
In the following scenario, input sizes are presumed randomly distributed between 1 and N. The distribution of lengths is pre-generated, and the same distribution is used for all hashes for a same N. This lean towards worst case scenario: generally, input sizes feature some kind of locality (as in target scenario, mostly between 20 and 30 bytes). But it gives us a good idea of how algorithms handle varying sizes.

This is a more significant victory for algorithms with an optimized access pattern. When input sizes become unpredictable, branch mispredictions become a much larger contributor to performance. The optimized access pattern makes the workload more predictable, and reduces the nb of branches which can be mispredicted. This is key to preserve a good level of performance in these conditions.
Throughput versus Latency
Throughput is relatively simple to measure : just loop over a bunch of inputs, hash them, then count the number of hashes completed in a given time.
But one could wonder if throughput is an appropriate metric. It represents a “batch” workload, where a ton of hashes are feverishly completed one after another. It may happen sometimes.
But in many cases, hashing is just one operation sandwiched between other very different tasks. This is a completely different background.
In this new setup, hashing must wait for prior operation to complete in order to receive its input, and later operation is blocked as long as the hash result is not produced. Hence latency seems a much better metric.
However, measuring latency is a lot more complex. I had many false starts in this experiment.
I initially thought that it would be enough to provide the result of previous hash as seed of the next hash. It doesn’t work : not only some algorithms do not take seed as arguments, a few others only use the seed at the very end of the calculation, letting them start hash calculations before the end of previous hash.
In reality, in a latency scenario, the hash is waiting for the input to be available, so it’s the input which must be based on previous hash result. After a lot of pain, the better solution was finally suggested by Felix Handte : use a pre-generated buffer of random bytes, and start hashing from a variable position derived from previous hash result. It enforces that next hash has to wait for previous hash result before starting.
This new setup creates a surprisingly different ranking :
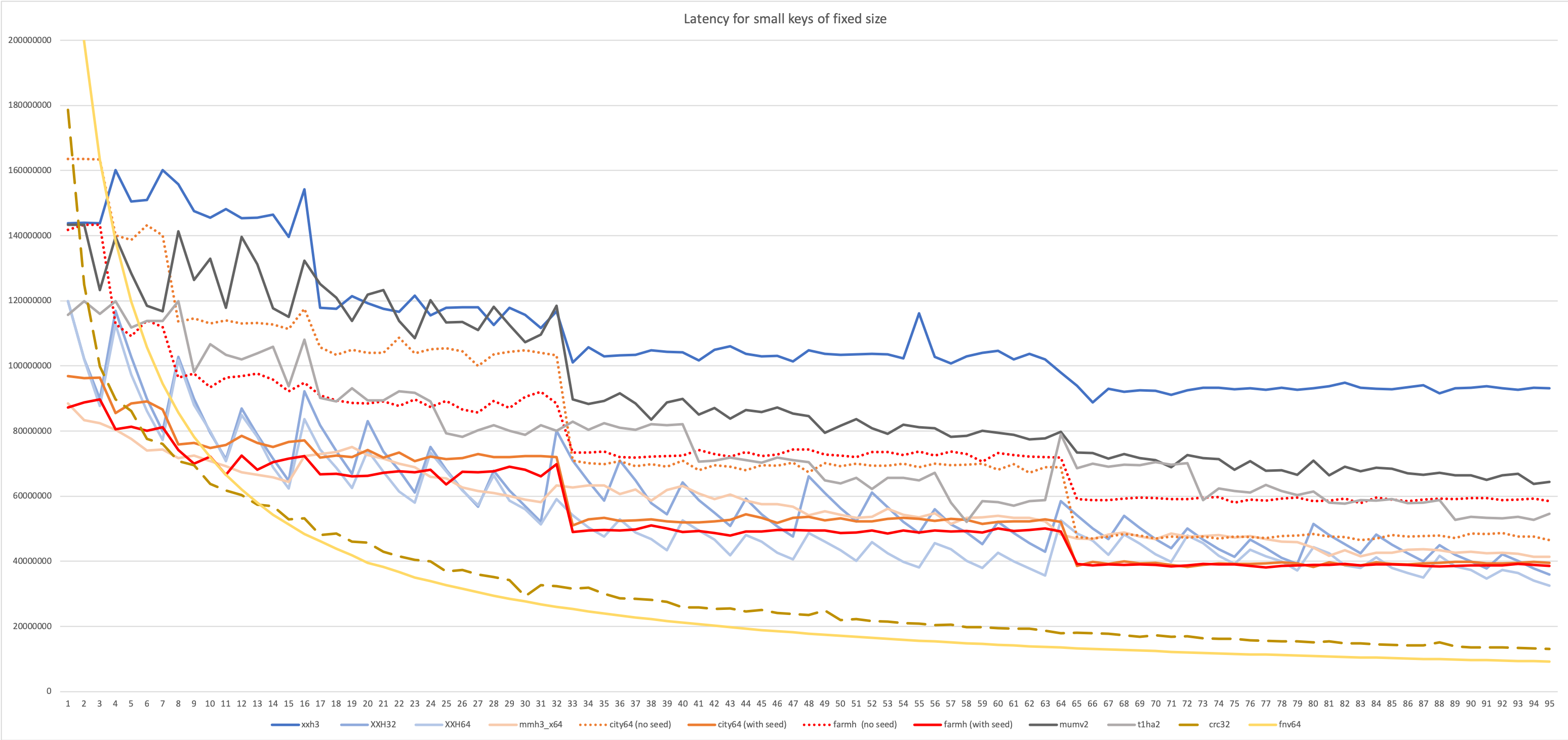
Measurements are a bit noisy, but trends look visible.
The latency-oriented test favors algorithms like Vladimir Makarov’s mumv2 and Leo Yuriev’s t1ha2, using the 64x64=>128-bits multiplication. This proved another source of inspiration for XXH3.
Cityhash suffers in this benchmark. Cityhash is based on simpler instructions, and completing a hash requires many more of them. In a throughput scenario, where there is no serialization constraint, Cityhash can start next hash before finishing previous one. Its simple instructions can be spread more effectively over multiple execution units, achieving a high level of IPC (Instruction per Clock). This makes Cityhash throughput friendly.
In contrast, the 64x64=>128-bits multiplication has access to a very restricted set of ports, but is more powerful at mixing bits, allowing usage of less instructions to create a hash with good avalanche properties. Less instructions translate into a shorter pipeline.
In the latency scenario, mumh2 fares very well, fighting for first place up to the 32-byte mark, after which XXH3 starts to take a lead.
However, this scenario involves fixed input size. It’s simple to code and explain, but as we’ve seen before, fixed size is actually an uncommon scenario : for most real-world use cases, input has an unpredictable size.
Hence, let’s combine the benchmark techniques seen previously, and look at the impact of random input lengths on latency.
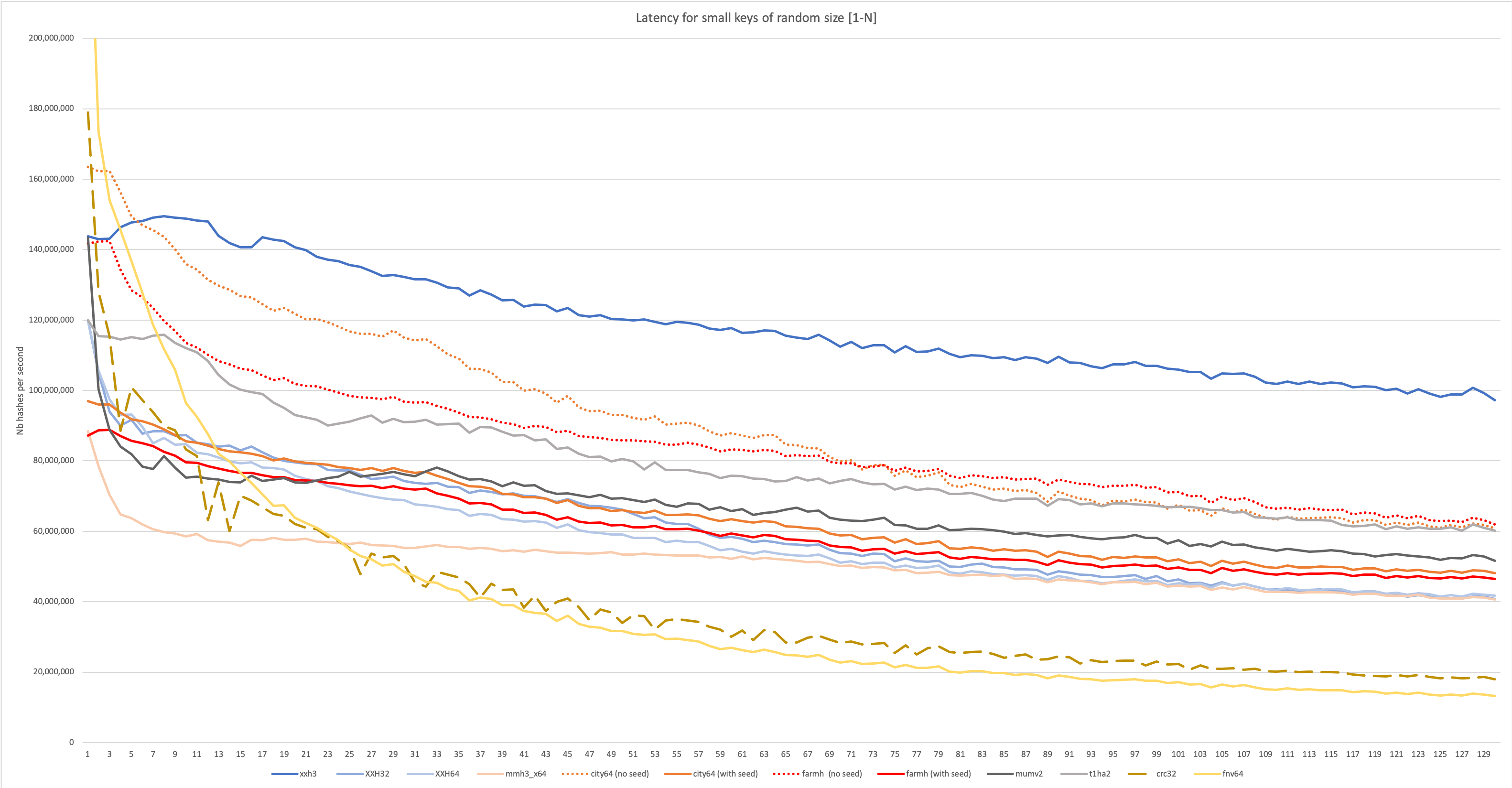
This is an important graph, as it matches the target use case of XXH3, and incidentally many real-world database/server use cases I’m aware of.
The variable size scenario favors algorithms using an optimized access pattern to reduce branch misprediction. mumv2, which was performing very well when input size was stable, loses a lot in this scenario. t1ha2 makes a better effort, and while not as well optimized as Cityhash for this purpose, loses nonetheless much less performance to variable input size, overtaking second place (if one does not count the “seed-less” variants in the ranking, due to afore-mentioned avalanche problems).
As could be expected, XXH3 is well tuned for this scenario. It’s no surprise since it was its target. So it’s basically mission accomplished ?
Hash Quality
It wouldn’t be a complete presentation without a note on hash quality. A good hash should make collisions as rare as possible, bounded by the birthday paradox, and offer great avalanche property : two different inputs shall produce vastly different output, even if they only differ by a single bit.
As expected, XXH3 completes all tests from SMHasher test suite. Both 64 and 128-bit variants were validated, as well as each of their 32-bit constituent.
But it went a bit farther.
SMHasher was designed many years ago, at a time when hashing was mostly a single main loop iterating over input. But as hash algorithms have become more powerful, this model feels no longer correct : modern hashes tend to feature a large inner loop, which is only triggered after a certain length. That means that the algorithm being tested when there are only a few input bytes is actually different from the one run on large inputs.
Because search space tends to explode with input size, and because computing capacity used to be weaker when SMHasher was created, most tests are concentrated on small inputs. As a consequence, tests for larger input sizes are very limited.
In order to stress the algorithm, it was necessary to push the tests beyond their usual limits. So I created a fork of rurban’s excellent SMHasher fork, methodically increasing limits to new boundaries. It’s still the same set of tests, but exploring a larger space, hence longer to run.
This proved useful during the design stage, eliminating risks of long-distance “echo” for example (when bits cancel each other by virtue of being at some exact relative position).
It also proved interesting to run these extended tests on existing algorithms, uncovering some “surprises” that were masked by the lower threshold of original tests.
To this end, these changes will be offered back to rurban’s fork, in the hope that they will prove useful for future testers and implementers.
Release
XXH3 is now released as part of xxHash v0.7.0. It’s still labelled “experimental”, and must be unlocked using macro XXH_STATIC_LINKING_ONLY. It’s suitable for ephemeral data and tests, but avoid storing long-term hash values yet. This period will be used to gather user’s feedback, after which the algorithm will transferred into stable in a future release.
Update: Since the release of xxHash v0.8.0, XXH3 is now labelled "stable", meaning produced hash values can be stored on disk or exchanged over a network, as any future version is now guaranteed produce the same hash value. Compared with initial release, v0.8.0 comes with streaming capabilities, 128-bit variant support, and better inlining.
This comment has been removed by the author.
ReplyDeleteYour chart shows that the xxh family has much greater (10x or more) throughput than crc32. Which crc32 implementation are you using? SIMD implementations can be around 14x faster than the crc32 implementation in zlib (the C library).
ReplyDeleteFor example, on my system (x86_64 Broadwell, clang 5, gcc 7, go 1.12, zlib 1.2.8), zlib-the-C-library (which doesn't use SIMD) clocks in at 1.3 GB/s:
$ git clone https://github.com/google/wuffs.git
...
$ cd wuffs
$ clang-5.0 -O3 test/c/std/crc32.c -DWUFFS_MIMIC -lz
$ ./a.out -bench -focus=mimic_crc32_ieee -reps=1 | grep ^Benchmark
Benchmarkmimic_crc32_ieee_10k/clang5 150000 8400 ns/op 1317.159 MB/s
Benchmarkmimic_crc32_ieee_100k/clang5 15000 75868 ns/op 1318.103 MB/s
$ gcc -O3 test/c/std/crc32.c -DWUFFS_MIMIC -lz
$ ./a.out -bench -focus=mimic_crc32_ieee -reps=1 | grep ^Benchmark
Benchmarkmimic_crc32_ieee_10k/gcc7 150000 8389 ns/op 1318.953 MB/s
Benchmarkmimic_crc32_ieee_100k/gcc7 15000 75747 ns/op 1320.220 MB/s
(Wuffs is https://github.com/google/wuffs, which is unrelated, other than it also implements zlib-the-format, and has a program to benchmark things like crc32. The key thing is the -lz, which means that it is measuring zlib-the-C-library. If you drop the "-focus=etc" arg, you can see that Wuffs' crc32 implementation is already 2x faster, without any SIMD.)
(To be continued, since comments are size-limited...)
The Go standard library's crc32 implementation uses SIMD, based on "Fast CRC Computation for Generic Polynomials Using PCLMULQDQ Instruction" https://www.intel.com/content/dam/www/public/us/en/documents/white-papers/fast-crc-computation-generic-polynomials-pclmulqdq-paper.pdf
ReplyDeleteIt can run more than 14x faster than zlib-the-C-library:
$ go test -test.bench=. hash/crc32 | grep IEEE
BenchmarkCRC32/poly=IEEE/size=15/align=0-56 30000000 48.8 ns/op 307.32 MB/s
BenchmarkCRC32/poly=IEEE/size=15/align=1-56 30000000 48.8 ns/op 307.27 MB/s
BenchmarkCRC32/poly=IEEE/size=40/align=0-56 30000000 43.5 ns/op 918.89 MB/s
BenchmarkCRC32/poly=IEEE/size=40/align=1-56 30000000 43.5 ns/op 920.43 MB/s
BenchmarkCRC32/poly=IEEE/size=512/align=0-56 30000000 46.9 ns/op 10926.26 MB/s
BenchmarkCRC32/poly=IEEE/size=512/align=1-56 30000000 46.8 ns/op 10930.01 MB/s
BenchmarkCRC32/poly=IEEE/size=1kB/align=0-56 20000000 76.4 ns/op 13395.03 MB/s
BenchmarkCRC32/poly=IEEE/size=1kB/align=1-56 20000000 75.9 ns/op 13499.42 MB/s
BenchmarkCRC32/poly=IEEE/size=4kB/align=0-56 10000000 228 ns/op 17941.81 MB/s
BenchmarkCRC32/poly=IEEE/size=4kB/align=1-56 10000000 231 ns/op 17720.61 MB/s
BenchmarkCRC32/poly=IEEE/size=32kB/align=0-56 1000000 1729 ns/op 18949.55 MB/s
BenchmarkCRC32/poly=IEEE/size=32kB/align=1-56 1000000 1668 ns/op 19642.23 MB/s
Chromium's copy of zlib-the-C-library also has its own SIMD implementation, based on the same "Fast CRC Computation etc" paper: https://cs.chromium.org/chromium/src/third_party/zlib/crc32_simd.c
I don't have the Chromium numbers readily available, but IIRC they were, unsurprisingly, comparable to Go's SIMD numbers.
Compared to all that, here's xxh3 on my system:
$ git clone https://github.com/Cyan4973/xxHash.git
...
$ cd xxHash
$ make
...
$ ./xxhsum -b
./xxhsum 0.7.0 (64-bits x86_64 + SSE2 little endian), GCC 7.3.0, by Yann Collet
Sample of 100 KB...
XXH32 : 102400 -> 67459 it/s ( 6587.8 MB/s)
XXH32 unaligned : 102400 -> 67189 it/s ( 6561.4 MB/s)
XXH64 : 102400 -> 134553 it/s (13139.9 MB/s)
XXH64 unaligned : 102400 -> 132667 it/s (12955.8 MB/s)
XXH3_64bits : 102400 -> 214190 it/s (20917.0 MB/s)
XXH3_64b unaligned : 102400 -> 201922 it/s (19719.0 MB/s)
So, out of the box (which means... SSE2 but no AVX2??), xxh3's top speed (20917 MB/s) seems roughly comparable to crc32's top speed (19642 MB/s). There certainly isn't an order of magnitude performance difference, once you use a modern crc32 implementation. :-)
Oh, the source code for Go's crc32 is:
Deletehttps://golang.org/src/hash/crc32/crc32_amd64.s
The Go asm language has its own peculiar syntax, neither Intel nor AT&T, as it descended from the highly portable Plan 9 assembler (Ken Thompson did both Plan 9 and Go). https://golang.org/doc/asm
In that file, "IEEE" and "Castagnoli" are alternative names for the crc32 and crc32c polynomials.
DeleteAh, if it's SMHasher's crc32 implementation, it's very simple indeed: https://github.com/aappleby/smhasher/blob/master/src/crc.cpp
ReplyDeleteI filed https://github.com/aappleby/smhasher/issues/70 but SMHasher's last commit was in January 2016, so it's not the most active of projects...
I've been using the latest version of `zlib`. It does multiple-bytes per round. I believe it's faster than default SMHasher's one.
DeleteYou mention the existence of a vectorized version of crc32. I was not aware of it. Up to now, I only found hashes which use hardware crc32c (which is different from "normal" crc32 as used in zlib).
Note that in this comparison, I've excluded hash functions which require specific hardware support.
It's not limited to Intel crc32c, there's also clmul and aes for example.
I could make a separate comparison including these variants, and make clear this is only representative of modern Intel platform, because most of them will suffer portability issues outside of it (generally, they have a software backup, so the issue is more about abysmal performance in absence of hardware support).
However, a "normal" crc32 which is vectorized would fit the bill.
I've looked at the chromium source code you linked to.
Good point : it doesn't use hardware crc32c ! That's really great !
Bad point : it uses clmul (carryless multiplier).
`clmul` is in a league of its own. It's not even part of sse/avx, it must be enabled with a specific compilation flag. So far, I've classified clmul as "specific hardware support", because no other platform support such an operation, so it's really Intel specific.
Nonetheless, if I get to make a comparison with hardware-supported hashes, this one would definitely fit the bill as a great crc32 implementation.
> I've classified clmul as "specific hardware support", because no other platform support such an operation, so it's really Intel specific.
DeleteTo be clear, AMD chips also support CLMUL, not just Intel. So says the internet:
https://en.wikipedia.org/wiki/CLMUL_instruction_set
> I've been using the latest version of `zlib`
DeleteIf you want to experiment with SIMD crc32, but it seems daunting to extract building Chromium's zlib from building all of Chromium, another option is to look at this (stand-alone) zlib fork:
https://github.com/jtkukunas/zlib/blob/master/crc_folding.c
I haven't tried it myself, and at first glance, the implementation seems longer than both Chromium's and Go's, but it is written by an Intel employee and references the same paper.
As for CLMUL requiring a specific compilation flag, this is no different from SSE4.2 or AVX, right? (x86_64 only implies SSE2, not SSE4.2).
DeleteSMHasher crc32 numbers, on my system:
ReplyDelete$ ./SMHasher crc32
...
Bulk speed test - 262144-byte keys
Alignment 0 - 0.166 bytes/cycle - 475.33 MiB/sec @ 3 ghz
Alignment 1 - 0.166 bytes/cycle - 475.32 MiB/sec @ 3 ghz
Alignment 2 - 0.166 bytes/cycle - 475.30 MiB/sec @ 3 ghz
Alignment 3 - 0.166 bytes/cycle - 475.31 MiB/sec @ 3 ghz
Alignment 4 - 0.166 bytes/cycle - 475.32 MiB/sec @ 3 ghz
Alignment 5 - 0.166 bytes/cycle - 475.32 MiB/sec @ 3 ghz
Alignment 6 - 0.166 bytes/cycle - 475.30 MiB/sec @ 3 ghz
Alignment 7 - 0.166 bytes/cycle - 475.31 MiB/sec @ 3 ghz
Normalizing 475 MB/s as 1.0x, we have the relative performance of several crc32 implementations:
1.0x SMHasher
2.8x zlib-the-C-library
41.4x Go's stdlib
So, when I said 14x, perhaps a more accurate number is 41x.
So, with long keys, you basically read 32-bit inputs and multiply them with some key material. Each 32-bit value gets "injected" only once. Why do you believe you can produce 128-bit hash this way? Intuitively, it seems that 32-bit inputs are reduced too quickly and do not exert a strong enough influence on the resulting 128-bit hash. Note that in FARSH, Bulat is clear that this scheme is only good for 32-bit result.
ReplyDeleteYes, you are correct. The 128-bits variant needs an additional stage. This will be fixed in next version.
DeleteThink what happens when the hash is used as a checksum and you need to detect a single error (the movie makers use case). Then, if data lanes are processed independently, and the error is limited to a single lane, the whole hash is only as good as a single lane. Other lanes do not whatsoever contribute to detecting the error. So you cannot "combine" the entropy from independent lanes at a much later stage, unless the lanes are wide enough.
DeleteYes, that's the plan, every bit of input will immediately influence 128-bit of accumulators. It is expected to satisfy this property.
DeleteIt's a pity that we don't have good collision estimator for 128-bit hashes. I can't think of a good way, to automate it, only algorithm analysis.
I just finished a project able to make good collision estimations for 64-bits hashes (it requires large resources, but that's reachable nowadays).
This might help at least to verify if a 128-bits hash only offers 64-bits of collision rate.
I've started a C# port here: https://github.com/Zhentar/xxHash3.NET
ReplyDeleteUnfortunately, my initial results are underwhelming for large inputs - even my SSE2 version is at just half the throughput of xxHash64, on par with xxHash32. I'm not sure yet what compiler heroics are getting you the speeds you're seeing (guess I'll have to deal with compiling it to see...), but my initial impression is that XXH3 will not port nearly as well as as xxHash32 & xxHash64 have.
It can be hard to access vectorial instructions. C is rather direct, but beyond that, all bets are off. Unfortunately, I have no experience to explain how to achieve the same impact with C#. I wish you good luck in your investigations !
Delete@unknown: You beat me to it. I ported xxHash64 and xxHash32 to C# some years back and it remains the fastest hash I know of.
Delete@Cyan: You probably already know about Intel VTune Amplifier. If not, it is a really good good tool to show the behavior of the CPU while running code. Cache-misses, hot paths, parallel execution etc. is all shown.
Yan
ReplyDeleteI've done some tests using xxhsum in a few ARM boards and the performance results of xxHashv3 are really awesome.
I think is really cool that you guys added a NEON optimized version in the first release, I wished more projects were paying attention to ARM processors given how dominant the architecture is on mobile.
I would assume that is just a matter of time to switch zstd to xxhv3? A good perf boost was achieved on Chromium's zlib by optimizing the checksums (i.e. crc32 and Adler-32) and leveraging SIMD optimizations.
Overall *really* solid work and thanks for sharing the code and the results with the community.
Best regards
Adenilson
The files for the graphs are missing
ReplyDeleteGood point @Harold !
DeleteThis is fixed now.
Graphs are also hosted on the project's wiki :
https://github.com/Cyan4973/xxHash/wiki/Performance-comparison
Hi Yann,
ReplyDeletefantastic speeds once more, congratulations!
I see you achieved 300,000,000 Keys/s hashing speed for 16..32 keys sizes, if you are interested I will include your fastest revision in my latest hash benchmark at:
https://github.com/wangyi-fudan/wyhash/issues/29#issuecomment-540811661
One of my laptops with i7-3630QM 3.4GHz achieved only ~4,000,000 Keys/s hashing speed + putting hashes into B-trees, thus I wanted to present a REAL-WORLD scenario not a synthetic one.
Could you point out or write a xxh3 variant suitable for 32bit hash lookups? My wish is it to return 32bit hashes.
Maybe, I misunderstand something, but no one seems to care to say that classic table-lookup hashers have little to do with strong hashes! To back up my words, please see the 3 tables in above link, wyhash is slower in '1001 Nights' to my superpoor (with significantly more collisions) FNV1A-Jesteress!
Seeing Wang Yi's approach and yours, which is faster for keys in range of 1..32 bytes?
Simply, want to include fastest lookuper into 'Lookuperorama' benchmark...
> Could you point out or write a xxh3 variant suitable for 32bit hash lookups?
ReplyDelete`XXH3_64bit()` should work fine for your needs.
It's expected that, for a table lookup, only a few bits are needed.
Feel free select the lower N or upper N bits as you wish, their distributions should be suitable.
> my laptops with i7-3630QM 3.4GHz achieved only ~4,000,000 Keys/s hashing speed + putting hashes into B-trees,
The B-tree is most likely way more cpu taxing than the hash, if only because of the (probable) cache misses that are generally associated with it.
> classic table-lookup hashers have little to do with strong hashes!
I agree
Played a little with 64bit, the quick result is the fastest known to me lookuper:
ReplyDeletehttps://gcc.godbolt.org/z/FoSSDb
Yann, smallkeyswise, can you tell whether there is room for improvement, I see none:
https://software.intel.com/en-us/forums/intel-moderncode-for-parallel-architectures/topic/824947#comment-1946638
Hi Yann,
ReplyDeleteWe are very impressed with the performance
when do expect that xxh3 64 bit would be stable for use persistently
thanks
There are 2 possible scenarios. Either :
Delete- Very soon : requires a minor refactoring of some corner cases (already identified).
- A bit later (but still this half) : investigate a larger refactoring involving the core loop. Undecided. Depends on cost / benefit trade-off.
I don't know at this stage which one will end up being selected. At the very least, and by default, I'll progress along scenario 1.
Thank for the response
Deletedo you expect that the return values will be changed or only performance
The return values for some corner cases will change.
DeleteCan xxHash and xxh3 be multithreaded? Does the core algorithm allow combining partial checksums from different sections of a sequential data stream?
ReplyDeleteYes, XXH3 can be.
DeleteIt's a bit complex though, as parallelism is limited to the block size (1 KB by default, can be increased by using a larger custom `secret`), and recombination of blocks must still happen in sequential order, to run the scramble stage (which has to be serialized).
That being said, the fact that `XXH3` is already faster than RAM on a single modern Intel core made it less useful to multi-thread it. As a consequence, there is currently no available implementation of multi-threaded `XXH3`.
Thank you for the quick response. I was thinking of many small cores but no SIMD support --the main intent of my question
DeleteYes, that's indeed a potential use case.
DeleteHow much quality loss would there be from computing a few (N) XXH3 128-bit hash values over portions of the original data (each with a separate seed), and then combining the result with XXH3? It seems like this a similar structure to the 4 internal state accumulators within a single XXH3 hash computation, except with a two-stage mixer at the end (N XXH3_128bits_digest() composed with 1 XXH3_128bits() rather than 1 XXH3_128bits_digest()).
ReplyDeleteIf I understand your question correctly, you would divide a content into blocks (B1, B2, B3, etc), calculate a checksum on each block, and then just combine them at this end (as a xor or add operation).
DeleteThe issue here is that this construction cannot detect changes in block order.
For example, if you have on one side (B1, B2, B3, etc.) and on the other side (B2, B3, B1, etc.), then they both get the same resulting hash. This is considered too weak.
This can be solved, by a stronger mixing stage, which ensures that (B1, B2) doesn't result in the same final hash than (B2, B1).
This is, by the way, how XXH3 works internally. One could already cut input into "blocks" (1 KB by default, can be extended by using custom seeds), compute them in parallel, and then combine them. The combine step though must be done serially, which ensures that each block must be provided in the correct order.
While this design is already possible, in practice, the reference library doesn't employ it, because the speed from a single thread is considered fast enough already (especially with vector instructions). But on weaker computing units, it could be a thing.
Varying the seeds across the blocks would be sufficient to differentiate them. I was also thinking that the final mixer would be XXH3_128(concat(H1, H1, ...)), which would also make the block hashes position-dependent.
DeleteIn my use case this isn't for parallelism purposes as much as pipelining, where I want to process a large number of B1, then a large number of B2, and the number of pending results is large enough that the size of the XXH3 streaming state is prohibitive.
Yes, that's an interesting design worth trying anyway.
DeleteThe xxHash repository also contains a large collision test, that would help to ensure the final design is resilient to basic collision expectations.
Hi, my use case for strings which are of 100bytes maximum. but no collision is very imp, I am making a decision to use xx128 so that collision possibility is ruled out. Any tool with which i can test around 100 billion string generation and check if collision occurs ?
ReplyDelete100 billion is really huge, one will need a lot of RAM to test that.
DeleteThere is also the important topic of filtering the input, and ensure that it does not feature identical strings, for the test to even be useful.
That being said, the Massive Collision tester, bundled as part of the xxhash project, could get you close to that. It's able to generate 100 billions binary objects which are guaranteed to be different, and will test and report the collision rate.
XXH128 has been tested with this tool by the way, and, as expected, it produced 0 collisions.
https://github.com/Cyan4973/xxHash/wiki/Collision-ratio-comparison